High Accuracy Mass Measurements
for Fundamental Symmetry Studies
The binding energy
of the atomic nucleus is certainly one of the most fundamental properties
of such many body systems. Accurate mass measurements serve as a testing ground
for nuclear models and stimulate their further improvement, and are required
for weak interaction studies in nuclear β-decay. Accurate mass measurements of high precision (δm /m < 10-8) on very short-lived
isotopes (T1/2 ≈ 50 ms) are needed
to experimentally test the theoretical corrections, which are employed to determine
Vud, the dominant matrix element of the
Cabibbo-Kobayashi-Maskawa (CKM) quark mixing
matrix. The CKM matrix should be unitary, based on fundamental concepts, however,
the present experimental results lead to Vud2+ Vus2+ Vub2 = 0.9740 ± 0.0014, [7]
which points to a 2.2 sigma deviation from the expected value. High accuracy
mass measurements would help to test the applied theoretical corrections for
the determination of Vud, and may ultimately
help determine, if the deviation from unitarity is
due to the reached precision or a nature-made effect. Should the effect be intrinsic
to nature, this would strongly imply ‘physics beyond the Standard Model’.
Table
1. List of envisaged candidates for precision mass measurements at TITAN. The
# indicates, that the mass is derived from extrapolations of systematic trends.
The expected yield and year is given, together with the production target and
ion-source (LIS=Laser Ion Source). Isotope Half-live Present
δm Expected
yield (year) Production odd-Z,
Tz=0 b emitters, with A ł 62 62Ga 116
ms 28
keV 5•103
2004 Zr
LIS 62Zn 9.1
h 10
keV 5•103
2004 Zr
LIS 66As 96
ms 200
keV 1•104
2003 Zr
ECR 66Ge 2.3
h 30
keV 1•104
2004 Zr
Plasma 70Br 79
ms 360
keV 5•105
2004 Nb
Plasma 70Se 41
min 210
keV 1•104
2005 Zr
Plasma 74Rb 65
ms 19
keV 5•103
2000 Nb
LIS even-Z,
Tz=-1 b emitters, with 18<A<42 26Si 2.21
s 3
keV 1•103
2006 TiC
ECR 30S 1.18
s 3
keV 1•103
2006 TiC
ECR 38Ca 439
ms 4
keV 1•103
2006 TiC
ECR/LIS 42Ti 200
ms 5
keV 1•103
2006 Ni
ECR
The mass measurement
of an ion confined in a Penning trap is accomplished by determining its cyclotron
frequency. For a particle with mass m
and charge q in a magnetic field B the cyclotron frequency is given by ωc = q/m •
B (or νc
= q/m • B/2p ) [12].
Therefore the observation of the cyclotron frequency for a particle with charge
q in a magnetic field allows one to quantify
the mass m. The magnetic field B is determined with an isotope of well known
mass. In an ideal case one employs 12C ions or 12Cx molecules [13],
where no experimental error is present, since these atoms are used for the unit
definition. The uncertainty δn of the resonance
frequency nc is given by the
Fourier limit which is inversely proportional to the observation or interaction
time TRF, hence δn ≈1/TRF. The deduced statistical mass uncertainty is
then given by: Where N is the number of detected ions. For
radioactive ions the factor TRF is fixed essentially
by the nuclear half-life. The number of detected ions N is depending on the
production yield and the available beam time. For existing Penning traps used
for high precision experiments, the magnetic field varies between 4 – 9 Tesla.
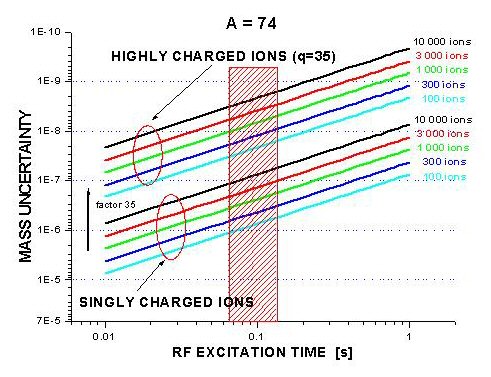
Therefore, the only way to increase Fig 3: Comparison of the achievable mass uncertainty
for 74Rb employing highly or singly charged ions. Shown are two sets
of curves, with various numbers of detected ions, as a function of excitation
time in the trap. Figure
3 shows clearly the gain factor in precision for the case of a mass measurement
for rubidium ions with mass 74, by storing highly charged ions (He-like, q=35+)
as compared to operations with singly charged ions, in a magnetic field of 6
T. Displayed in the box in the graph is an excitation time corresponding to
two half-lives, which is a practical assumption, given the fact, that single
ions are prepared and observed in the Penning trap. With the already proven
production rate of 74Rb at ISAC of 14000 ions/s, an interaction time
for the mass measurement of T = 100 ms, and the total efficiency of the proposed
set-up including nuclear decay losses to be e= Ľ % the required beam
time to reach the aimed for mass accuracy is calculated to be only a few minutes.
The absolute mass uncertainty for 10 000 detected ions of 74Rb 35+ would
in this case be δm ≈ 200 eV.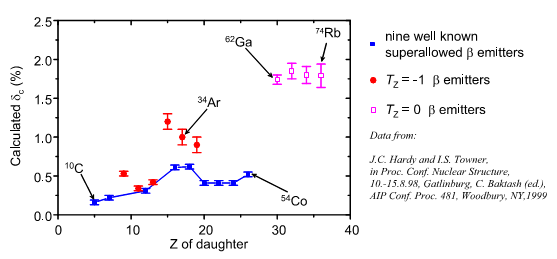
Fig 2: Calculated contribution of theoretical corrections dC to the ft value. The data
of the nine well known superallowed b emitters are connected, where the others, not connected
points are the new proposed b emitters,
where complete experimental data sets not yet exist.
![]() The
experimental data needed are the ft values for superallowed
b transitions. These allow one to determine
Gv, the vector coupling constant, which
then can be used to determine the Vud matrix
element for the up-down quark mixing. Gv
can basically be obtained from the experimental ft values and employing the
well-known relationship which is true for 0+ ® 0+ b transitions. f is the statistical rate function, t is the partial half-life
for the transition. FT is defined as the corrected ft value, were isospin
symmetry breaking correction dC and the transition-dependent part of radiative
correction dR are applied.
DVR is the radiative
correction part that is independent of the transition, and K is a constant.
In order to be able to determine the source of the deviation from unitary, one
needs to exclude the possibility of erroneous theoretical corrections. To test
this, the experimental precision has to be better than the theoretical corrections
applied [8].
For the partial half-live, the experimental achievements have been demonstrated
on this level of precision [9]
and are even further developed [10].
The
experimental data needed are the ft values for superallowed
b transitions. These allow one to determine
Gv, the vector coupling constant, which
then can be used to determine the Vud matrix
element for the up-down quark mixing. Gv
can basically be obtained from the experimental ft values and employing the
well-known relationship which is true for 0+ ® 0+ b transitions. f is the statistical rate function, t is the partial half-life
for the transition. FT is defined as the corrected ft value, were isospin
symmetry breaking correction dC and the transition-dependent part of radiative
correction dR are applied.
DVR is the radiative
correction part that is independent of the transition, and K is a constant.
In order to be able to determine the source of the deviation from unitary, one
needs to exclude the possibility of erroneous theoretical corrections. To test
this, the experimental precision has to be better than the theoretical corrections
applied [8].
For the partial half-live, the experimental achievements have been demonstrated
on this level of precision [9]
and are even further developed [10].
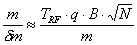
 the
accuracy by a large factor at given nuclear half-life or to access much shorter-lived
isotopes at a constant accuracy aimed for is to increase the charge state q
of the ion investigated. Here, a large factor can be gained. The path to reach
high accuracy mass measurements (δm /m ≈10-8)
even on rather short-lived isotopes (T1/2 = 50 ms) is to use a Penning
trap system, in combination with a charge breeding device at an ISOL-facility.
The potential of this concept has been demonstrated by the SMILE-TRAP at
the
accuracy by a large factor at given nuclear half-life or to access much shorter-lived
isotopes at a constant accuracy aimed for is to increase the charge state q
of the ion investigated. Here, a large factor can be gained. The path to reach
high accuracy mass measurements (δm /m ≈10-8)
even on rather short-lived isotopes (T1/2 = 50 ms) is to use a Penning
trap system, in combination with a charge breeding device at an ISOL-facility.
The potential of this concept has been demonstrated by the SMILE-TRAP at
