Click here for a printable PDF version
Penning Traps
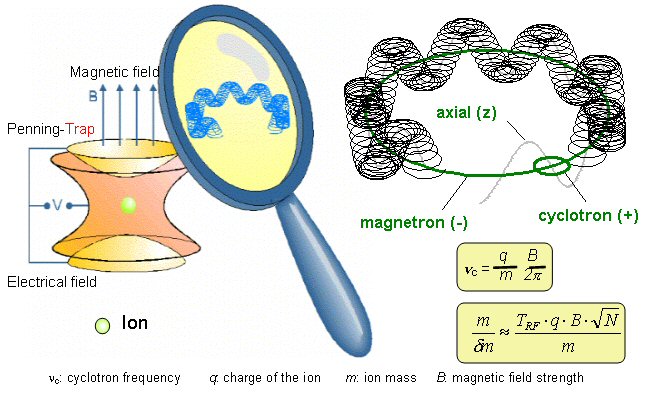
In a Penning trap ions are confined in 2-D via the application of a strong magnetic field. A weak electrostatic field is then applied so as to trap ions in 3-D.
The penning trap has proved to be a useful tool in mass spectrometry and has been used to make the most accurate measurements of the masses of a number of stable nuclei. However in order to reduce the statistical uncertainty in the measurement of a mass in such a trap it is necessary to store the ions for relatively long times (~ minutes to hours). The TITAN project aims to measure the masses of short lived radioactive nuclei (t1 / 2 = 50ms) and so it is clear that it is not possible to store such ions for long periods of time. It is however possible to obtain the required reduction in statistical uncertainty by injecting highly charged ions into the trap.
Consider a highly charged ion with low energy that moves in a strong magnetic field. The ion will have a cyclotron motion with cyclotron frequency:
w c = [ q/m]B
Where q is the charge on the ion and m is its mass.
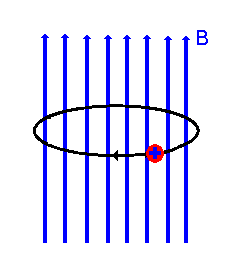
So if we know the strength of the B-field and the charge on the ion it is clear that a measurement of the cyclotron frequency will give us all the data we need to find the mass.
So how do we measure the cyclotron frequency? First we must trap the ions in 3-dimensional space. The application of a B-field traps the ion in 2-D and by the application of a weak electric field we can trap the ions in the remaining dimension.
We would like the motion in the trap to be as simple as possible and so would like to apply a force on the ions which is proportional to the distance of the ions from the center of the trap and which does not affect the ions 2-D cyclotron motion. Such a force is provided by a harmonic potential in 3-D with the form:
|

This is realized by a 3 electrode configuration. The two end cap electrodes
are hyperboloids of revolution around the Z-axis and the ring electrode also
has a hyperbolic cross section.
This electrode configuration can be used to trap ions with respect to the Z-axis and cause the ions to oscillate with a simple harmonic motion.
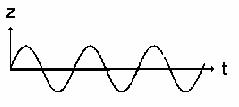
By applying a B-Field along the Z-axis the ions will have a cyclotron motion in the X-Y plane commonly known as the magnetron motion. The ions will also undergo a second smaller (reduced) cyclotron motion due to the effects of the applied electrostatic field. So the resultant motion looks like:
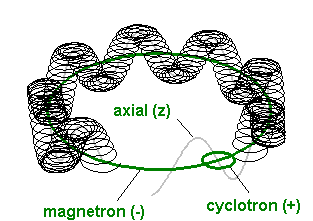
If we now apply an RF-field with resonant frequency equal to the product of the frequencies of the magnetron and cyclotron motions a coupling of the two motions occurs such that a periodic conversion from one to the other takes place. If we now extract the ions from the trap and accelerate them toward a target their time of flight between the trap and the target is related to their radial energy in the trap. From this information we can tell if the cyclotron and magnetron motions are coupled. The frequency of the RF can then be used to find the mass of the ions.

Typical experimental Time of Flight distribution
The resolution of such a mass measurement made in such a trap is given as:
|
We see that injecting a large number of ions with a high charge state into the trap will improve the resolution. TITANs unique combination of an RFQ, EBIT and precision Penning trap will allow us to do just this with a predicted resolution = 10-8.
Recommended Further Reading
Text Book
P.K.Ghosh, Ion Traps, Oxford University Press, 1995
