Standard Model

There are four types of forces known in the universe. The Standard Model deals with three of them, the electromagnetic force, weak nuclear force and strong nuclear force because all attempts to incorporate the gravitational force have failed so far. The Standard Model states that all matter is essentially constructed from particles with a spin of called fermions. The category of fermions is divided into two groups: quarks and leptons. Each of these groups contains 6 flavours or types of either quarks or leptons.

Leptons:

Leptons exist as free particles and can be either negatively charged or neutral.\A0 The leptons with a negative charge are: electrons, muons, and tauons.\A0 Muons and tauons are heavy versions of the electron, so heavy in fact that they are unstable and decay rapidly into electrons, neutrinos, and other particles.\A0 Neutrally charged leptons are called neutrinos.\A0 Each neutrino has a charged lepton partner and is written with that corresponding flavour in subscript (i.e. ν_e for electron-type neutrino).

Quarks:

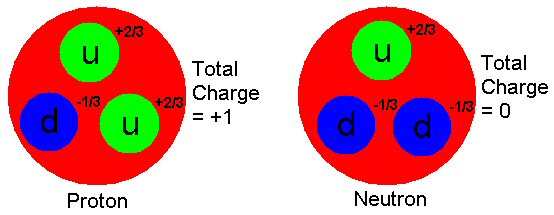
Quarks don\92t exist as free particles, and as such can occur fractionally charged.\A0 As with the leptons these can be broken up further into two categories of charge.\A0 The quarks with a charge of +2/3 are: up, charmed, and top.\A0 The quarks charged with a value of -1/3 are: down, strange, and bottom.\A0 Quarks are found in combinations of quarks.\A0 Protons and neutrons are formed by combinations of three quarks each.\A0 Protons consist of one down and two up quarks resulting in a charge of +1.\A0 (2/3 + 2/3 \96 1/3 = +1)\A0 Neutrons consist of one up and two down quarks resulting in a charge of 0.
(2/3 \96 1/3 \96 1/3 = 0)

Interactions Between Fermions

Fermions exchange particles of integral spin called \93bosons\94 to interact with one another in different types of interactions:

Strong: -binds together for example the quarks in the neutrons and protons as well as the protons and neutrons with each other inside nuclei
-mediator is the gluon, a massless particle
Electromagnetic: -binds charged particles, for example the e^- to nuclei
-responsible for the intermolecular forces in liquids and solids
-mediated by the exchange of photons
Weak: -β-decay involving a radioactive nucleus emitting an electron and neutrino is mediated by the W^\B1 and Z⁰ bosons

It has been thought that these different fields of interaction are different aspects of a single unified field.\A0 In the 1970\92s it was found that at very high energies weak and electromagnetic interactions have the same strength, and can therefore be unified with each other to form the electro-weak force.

CKM Matrix

Quarks can change into another type or \93flavour\94 of quark via weak interaction.\A0 The charge of a quark may only be changed by one unit of elementary charge e.\A0 Because of these circumstances, each of the quarks with a charge of +2/3 (up, charm, top) may change into any quark with a charge difference of e (down, strange, bottom).\A0 We now have 9 different possible transformations that may occur.\A0 When a top quark transforms into a bottom quark we may consider this a \93pairing.\94\A0 Each pairing has its own weak charge attached to it, which is related to a physical constant called the \93coupling constant.\94\A0 We can take these 9 coupling constants and place them in a 3x3 matrix like this:

  Here V_ud , for example,\A0denotes the coupling strength from an up-quark into a down-quark and vice versa. 

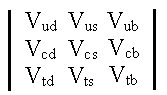
This is called the Cabbibo-Kobayashi-Maskawa (CKM) matrix after three Japanese men. The CKM matrix relates the weak eigenstates with the strong eigenstates.\A0 Using this matrix, we can find the probability of any given quark changing into another.\A0 If we define the probability of an up quark transforming to a down quark as being V_ud², then all possible transformations for the up quark can be written as: V_ud² + V_us² + V_ub² = 1.\A0 In this framework these values add up to one, however experimental evidence is not that clear.\A0 With experiments in nuclear physics, particularly at ISAC/TRIUMF which is the one we have access to, with unstable radioactive nuclei produced online, we mainly look at the up-quark.\A0 Top quarks for example are difficult to produce and therefore top quark transformations are not observed as often.\A0 The experimental values for the CKM matrix as of 2002 are:

 
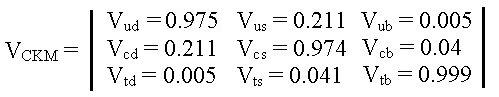
In fact a 2.2 σ deviation from unity is presently found.

\83t Value

The ft-value represents a transition strength of the weak-or beta-decay. It consists of an energy dependent Fermi integral, the f-value, and the half-live of the transition of interest, the t-value. The ft-value is directly coupled with the CKM matrix element of the relevant transition. In nuclear physics this corresponds to the V_ud elements, where the coupling of an up to a down quark is described. An experimentally derived ft value should now allow one to determine the up-down coupling. However, the nuclear environment, in which the decay occurs, requires the \91simple\92 formulation to be altered by introducing theoretical correction, namely radiative and Coulomb corrections.\A0

Theoretical Corrections

We need theoretical corrections when we measure things at a subatomic level because everything happening outside the system we are trying to measure affects the system itself.\A0 We will talk about two different types of theoretical corrections: radiative and Coulomb.

Radiative Corrections:

Radiative corrections are there to account for the processes allowed by Quantum Electro Dynamics (QED) occurring in the vacuum and within the nucleus itself.

Coulomb Corrections:

They account for the electroweak interactions affecting the system we are attempting to measure.\A0 For example, if we are trying to measure some aspect of the β-decay of a neutron we may concentrate our measurement on solely the neutron of interest, however outside that neutron there may be other particles interacting with the neutron.\A0 Coulomb corrections attempt to estimate the effect of these particles on the neutron of interest but since we cannot accurately know how these particles interact with each other and the neutron, the Coulomb corrections can vary.